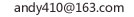怎样才能将正五边形分成全等的五部分（三种方法）

找到正五边形的中心，
1.由中心向边作垂线
2.中心连结顶点
3.五边同一方向(顺或逆时针)取一等量点，连结这些点与中心

不只发噢，。； 妯

如何将正五边形分成全等的五部分(用三种方法)~

图中的相邻两条虚线的夹角：
360÷5＝72°
这样的分法有无数种，
首先要确定正五边形的中心点，
从任意两个顶点向对边中点作直线，
两条直线的交点就是正五边形的中心点

#15281443070# 在一个五边形的花园里,要怎样修建小路才能使这些小路正好把花园分成5个全等的三角 - ******
#越从#[答案] “璐过·幸福”: 如果这个花园是个凸正五边形. 作任意二条边的垂直平分线,相交于一点,这个点就是这个凸正 五边形外接园的园心,将这个圆心分别与五个顶角连接,就把花 园分成五个全等的三角形. 祝好,再见.

#15281443070# 简单数学题在一个五边形的花园里,要怎样修建小路才能使这些小路正好把花园分成五个全等三角形? 如果要分成10个三角形呢? - ******
#越从#[答案] 分成五个全等三角形只要取五边形里面的中点然后连接各顶点 分成10个三角形只要在刚才的基础上由中点作各边的高 就OK了

#15281443070# 在平面上画出五个正五边形,最多可以把平面分成几部分? - ******
#越从#[答案] 这个要画图回答哦. 我会这题. 电脑里那图形咋画额. 这么说吧.要是那个平面图是圆的话6条直线12部分.N条就是2n个部分. 应该是对滴.可能说的不明白- -~! 我不会讲题哦. YOU滴——XX (*^__^*) 嘻嘻……

#15281443070# 如果在一个平面上画出4个正五边形,最多可以把平面分成几个部分?要算式, - ******
#越从#[答案] 32我自己数的如果上一题也是你出的话,那题是20

#15281443070# 求证正五边形的五条对角线都相等. - ******
#越从#[答案] 利用三角形全等的性质,正五边形的五条边都相等,五个内角也都相等.每两个边及其所夹内角和一条对角线组成一个三角形,根据三角形两边及夹角分别相等的全等条件,五个三角型都全等,则,五条对角线都相等

#15281443070# 将一个圆平均分成5份(尺规作图) - ******
#越从#[答案] 就是那个画正五边形的尺规作图法了: 设圆心为O 过O作两条互相垂直的直径AB,CD 以AC为半径作圆弧交AB于E 则,CE就是圆内接正五边形的边长.用它来可以将圆周截为平均的五分.

#15281443070# 正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应() - ******
#越从#[选项] A. 把圆n等分,顺次连接各分点得到的多边形是圆的内接正n边形 B. 把圆n等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形 C. 各边相等.并且各角也相等的多边形是正多边形 D. 用量角器等分圆是一种简单而常用的方法

#15281443070# 正五角星的内角和是多少度要有步骤,有过程 - ******
#越从#从图中我们看出,正五角星的顶点就是正五边形的顶点,这样我们发现正五边形的顶点将圆周分成五等份,每等分的度数等于360÷5=72°,因此正五角星的每个内角的度数等于72÷2=36°,因此,36*5=180°

正五边形有多少条对角线?多少条对称轴

可以与其余2个顶点构成对角线。由于每条对角线被计算了两次，所以实际的对角线数量为5条。对称轴：正五边形有5条对称轴，这些对称轴都经过正五边形的中心，并且连接中心与各个顶点。这些对称轴将正五边形分成5个全等的等腰三角形，验证了正五边形的对称性和均匀性。

求证正五边形的五条对角线都相等.

利用三角形全等的性质，正五边形的五条边都相等，五个内角也都相等。每两个边及其所夹内角和一条对角线组成一个三角形，根据三角形两边及夹角分别相等的全等条件，五个三角型都全等，则，五条对角线都相等

怎么把一个五边形分成十五份

等腰三角形底边三等分。由五边形外接圆的圆心向五个顶点连线，把五变形分成五个全等的等腰三角形，外接圆半径等于腰长。把每个等腰三角形的底边三等分，连接两个等分点和等腰三角形顶点，把等腰三角形分成三个三角形，这三个三角形等底同高面积相等。这样就把正五边形15等分。一共连15条线。

正五边形有几条对角线?

正五边形有15条对角线。正五边形是指五条边长度相等，且五个内角均为108°的五边形。对于正五边形，从中心向任何一个顶点引对角线，可以把正五边形分成两个全等的等边三角形，因此正五边形有5条对角线。此外，正五边形还有10条边，每条边对应的对角线有两条，因此还有10条对角线。因此，正五边形共有15...

怎样判定五边形全等不是定理

这两个图形必须完全重合才能全等对吧！所以说判定五边形全等就要证明对应边相等，对应角也要相等，这就很复杂了！如果是判定正五边形全等那就只要证明这两个五边形的边长相等就可以了。

正五边形有几条对称轴怎样画?

5条，如果五边形不正，只有一条对称轴 把一张纸对折，两侧的纸能完全重合，这就叫轴对称图形，如图1，正五边形有5条对称轴。如果正五边形太长或太扁，就像长方形一样，就不叫正五边形了，正五边形太长或太扁都只有1条对称轴。

一个正方形,怎样才能剪成五个角?

有三种剪法。分别阐述如下：（1）剪法一，剪去一个小角，此时正方形剪完后有五个角。如下图所示：（2）剪法二，通过一个顶点剪去一个角，此时正方形剪完后有四个角，是一个直角梯形。如下图所示：（3）剪法三，沿着对角线剪，此时正方形剪完后有三个角，是一个三角形。如下图所示：...

正六边形和正五边形的区别

正六边形的每个内角为120°。正五边形的每个内角为108°。内角和不同：正六边形的内角和为720°。正五边形的内角和为540°。轴对称图形的角线条数不同：正六边形有6条对称轴，每条都通过一个顶点和相对边的中点，将图形分为两个全等的部分，因此也有6条角平分线。正五边形有5条对称轴，同样地，每条都...

证明正五边形对角线相等的思路 求.

利用三角形全等的性质,正五边形的五条边都相等,五个内角也都相等.每两个边及其所夹内角和一条对角线组成一个三角形,根据三角形两边及夹角分别相等的全等条件,五个三角型都全等,则,五条对角线都相等.(本人非数学专业,仅供参考）

圆内接正五边形的画法证明

1、圆内接正五边形五条边长度相等。（即圆的五条弦长度相等）。2、圆内接正五边形的五个内角相等，都是108°。3、圆内接正五边形的五条边在圆内所对的五条优弧长度相等。4、圆内接正五边形的五条边在圆内所对的五条优弧的弧度数相等。