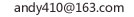这个问题的基础还是之前提到的梁氏三分角定式操作. 原理是,五等分后中间部分的角度,既是上部的1/3,又是下部的1/3。 因此,五等分任意角可以看作是三等分任意角的延续。下图附梁氏三分角定式操作.
1,作角弧AB,并直线连结AB
2,作角平分线交弧AB于点a,交AB于点b.
3,以A为圆心AB长为半径作弧,以B为圆心Ba长为半径作弧,两弧相交于点c.
以B为圆心BA长为半径作弧,以A为中心Aa长为半径作弧.两弧相交于点d.
4,直线连结cd,cd平行于直线AB.直线连结bc,bd.
5,在bB上取点e,在cd上取点f,be:cf=5:12.直线连结ef交bc于点C.同上在bd上截取点D.角COD=角1/5AOB.
6,作角BOC,AOD平分线.即可
此法也存在误差
请问怎样用尺规将一个角(任意角)五等分?~
1,作角弧AB,并直线连结AB
2,作角平分线交弧AB于点a,交AB于点b.
3,以A为圆心AB长为半径作弧,以B为圆心Ba长为半径作弧,两弧相交于点c.
以B为圆心BA长为半径作弧,以A为中心Aa长为半径作弧.两弧相交于点d.
4,直线连结cd,cd平行于直线AB.直线连结bc,bd.
5,在bB上取点e,在cd上取点f,be:cf=5:12.直线连结ef交bc于点C.同上在bd上截取点D.角COD=角1/5AOB.
6,作角BOC,AOD平分线.即可
~~~
此法也存在误差
三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一,即 用圆规与直尺把一任意角三等分。问题的难处在于作图使用工具的限制。古希腊人要求几何作图只许使用直尺 (没有刻度,只能作直线的尺)和圆规。这问题曾吸引着许多人去研究,但都无一成功。1837年凡齐尔( 1814-1848)运用代数方法证明了,这是一个标尺作图的不可能问题。
在研究「三等分角」的过程中发现了如蚌线、心脏线、圆锥曲线等特殊曲线。人们还发现,只要放弃「尺 规作图」的戒律,三等分角并不是一个很难的问题。古希腊数学家阿基米得(前287-前212)发现只要 在直尺上固定一点,问题就可解决了。现简介其法如下:在直尺边缘上添加一点P,命尺端为O。 设所要三等分的角是∠ACB,以C为圆心,OP为半径作半圆交角边于A,B;使O点在CA延在线移 动,P点在圆周上移动,当尺通过B时,连OPB。由于OP=PC=CB,所以∠COB=∠AC B/3。这里使用的工具已不限于标尺,而且作图方法也与公设不合。
#15788808130#
请问怎样用尺规将一个角(任意角)五等分? - ******
#任费# 第一次作角平分线,得2个角,再分别作两条角平分线即可.
#15788808130#
尺规作图怎样用尺规作一个角,使这个角的度数是原来已知角度数的两倍 - ******
#任费#[答案] 以角的顶点做一个圆, 圆于角的两边分别有一个交点, 截取两个交点之间的长度,以任意一个交点为圆心画圆 两个圆会有另外一个交点出现 连结角的顶点和这个交点,那么得到的角度就是原来角度的两倍
#15788808130#
利用尺规作图可将任意角分成几等分利用尺规作图可将任一角分成几等分 - ******
#任费#[答案] 对于这个问题我们应该从古希腊三大几何问题之一的用尺规三等份任意角问题说起接下来阿基米德将直尺沿直线CPB平行移动,使C点正好移动到O点,并作直线OD.
#15788808130#
如何作一个角等于已知角?用尺规作图法 - ******
#任费#[答案] 例如 已知:∠AOB.求作:一个角,使它等于∠AOB.步骤如下::(1)作射线O′A′(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D(3)以O′为圆心,以OC的长为半径画弧,交O′A′于点C′(4)以点C′为圆心,以CD的长为半...
#15788808130#
由已知角用尺规作一个相同的角该怎么作? - ******
#任费#[答案] 方法很多的,你先自己想想 比如,随便画一条线将这个角A变成三角形ABC,然后“复制”这个三角形:也就是说,复制一条边AB,到A'B',然后分别以A'为端点,AC为半径、以B'为端点,BC为半径画弧,两条弧的交点记作C',那么A'B'C'和ABC...
#15788808130#
如何用尺规作一个角等于已知角 - ******
#任费#[答案] 假定已知角∠A,∠A的两个边a,b. 以A为圆心画个圆,圆和a,b相交C,D,连接CD. 接着画需要的角 先画条射线e,顶点是E.以E为圆心,AC为半径画个圆1,圆1和e相交于F,以F为圆心,CD为半径画圆2,圆1和圆2有两个交点,任选一个,假设是G,...
#15788808130#
如何尺规作图三等分任意角 - ******
#任费# 三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一,即 用圆规与直尺把一任意角三等分.问题的难处在于作图使用工具的限制.古希腊人要求几何作...
#15788808130#
如何 用尺规做一个等于90°的角 - ******
#任费#[答案] 请问有原图吗?比如说他给你出了这道题,并给你画上了个90°的角,让你用尺规做与之相等的角,如果有,那就这样做:
#15788808130#
如图,已知用尺规将三等分一个任意角是不可能的,但对于一些特殊角则可以利用作等边三角形的方法三等分,请用直尺和圆规把平角CDE和∠AOB=45°这... - ******
#任费#[答案] 如图所示,射线DM、DN为平角CDE的三等分线; 如图所示,射线OP、OQ为∠AOB=45°三等分线.
#15788808130#
如何用尺规作一个角等于已有的角? - ******
#任费#[答案] 先画一条直线,用量角器量出已知角的大小,再在直线取端点,用量角器在此端点上与已知角相等画出一点,连接端点与直线.就可以了